¡Un nuevo comando para hacer los applymovements dinámicos y fáciles! El MoveObjectToPos().
Este nuevo comando sirve para los proyectos de decompilación. En particular, fue realizado para pokeemerald.
¡A partir de ahora, no tendrás que liarte con tantos applymovements, solamente dile al mini a donde tiene que moverse y lo hará! Pero ¿De dónde viene todo esto?
El aburrido y confiable Applymovement:
Bien, supongamos que tenemos esto: Un mapa lleno de objetos y minisprites y queremos coreografiar una escena con applymovement. Es un dolor de cabeza estar contando pasos, haciendo que el mini en cuestión se mueva los pasos necesarios, no se sobreponga con otros objetos y que respete las reglas del terreno. Y bueno, ahora imaginemos que queremos que el protagonista pueda activar el script de desde varias posiciones… ¿Cómo es que hacíamos todo de forma tradicional? Pues a punta de condicionales, contando pasos y creando secuencias personalizadas para cada posibilidad… O también tenemos al loquillo de turno que ponía un pasillo de un solo espacio para no poner gatillos….
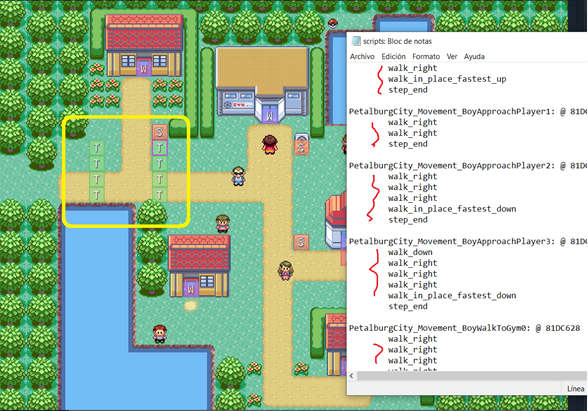
¿Y si hacemos algo más robusto?
Ahora bien, digamos que ya tienes tu coreografía lista y todo como debe ser…. Pero se te ocurre cambiar el mapeado… Bien, pues se te van a ir los applymovements al carajo.
¿Y si te dijera que se puede tunear el applymovement de tal manera que solo tengas que poner las coordenadas finales del objeto en cuestión?
Técnicamente podríamos calcular las coordenadas del mini, restarlas por las coordenadas de destino que queramos y moverse «x» casillas a la derecha o a la izquierda dependiendo del signo y «y» verticales hasta llegar al destino.
Sería un algoritmo fácil de ejecutar y se comportaría bien en mapas abiertos y donde no importen mucho los obstáculos.
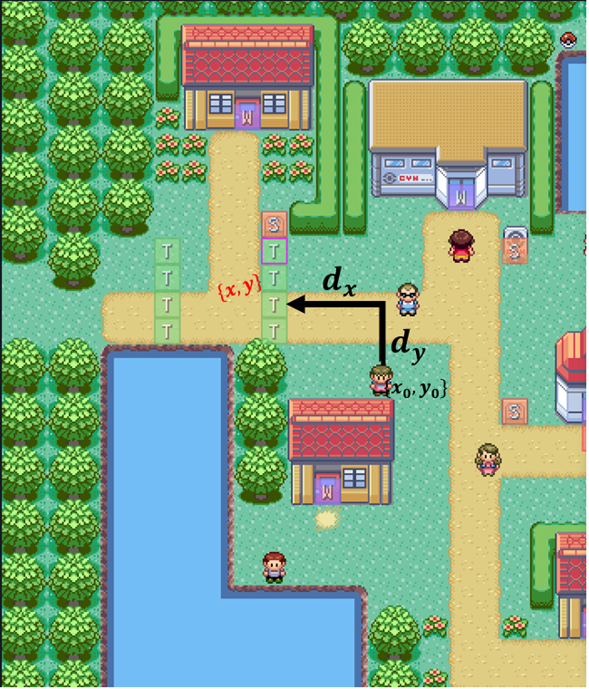
En el caso del chico de Petalia quedaría bastante bien: en vez de tantas líneas de código y condicionales dependiendo de cada gatillo, se podría hacer que cada gatillo ejecutara el mismo script de leer las coordenadas del prota y mover al chico a esas coordenadas (bueno restando una casilla, que hay que respetar el espacio personal ¿Qué no les enseñan urbanidad en la casa? ¡Caramba!)
Un comando así podría ser tan sencillo como:
MoveObjectToPos(IdObject, X, Y, Facing)
Donde el IdObject representa el ID del mini a mover, X y Y la coordenada final y el facing un comando opcional para que luego del movimiento el mini quede apuntando hacia alguna dirección.
Vale, pero ¿Cómo hacemos cuando hay obstáculos en el camino?
Para casos más generales esta solución no es suficiente y es necesario tener en cuenta el mapa en sí mismo, al igual que los obstáculos, otros minis y las elevaciones del terreno.
Y para esto entra a ayudarnos nuestra querida amiga la Inteligencia Artificial.

Básicamente, se implementó un algoritmo de
Aquí les dejamos unos ejemplos del camino que elige, esquivando obstáculos como tiles u otros minis. Lo único que se le pone al comando son las coordenadas del destino:


¿Vale y como uso esto en mi proyecto?
Puedes echarle un vistazo a mi fork haciendo click aquí. ¡Eso sí, aún no está listo y por favor no lo vayas a incorporar a un proyecto serio! Sigo haciendo pruebas con el algoritmo y no lo he vuelto aún un comando. De momento puedo llamarlo con un callnative y añade los parámetros manualmente en las líneas indicadas aquí.
¿Cuándo estará lista una versión que pueda meter en mi proyecto?
Pronto, digamos que, en una o dos semanas, por supuesto, haré un anuncio en el foro y un tutorial de cómo utilizarlo.
¿Qué le hace falta?
• Que funcione como un comando normal de cualquier script y no como un callnative (para eso me va a ayudar el bueno de Samu que tiene experiencia con esto).
• Como han visto, la cantidad de nodos explorados y operaciones aumenta exponencialmente con el número de tiles. Aún no lo he probado en mapas muy grandes y creo que podría hacer overflow de memoria.
• Quisiera evitar lo anterior haciendo algunas listas dinámicas (que no les tenga asignar un máximo número de nodos desde antes) y que evite hacer movimientos en las zonas fuera de la pantalla de carga. Esto reduciría el mapa sobre el que explora el camino muchísimo más y evitaría los problemas de overflow.
• Adicionalmente, quiero añadir que pueda atravesar zonas de diferente altura, calculando su propia altura durante el movimiento (y no desde el principio como lo tengo ahora) y así pueda subir a puentes y saltar barrancos o usar tiles por los que solo se pueden pasar en un sentido.
Además de applymovements fáciles, ¿Para qué más podría usarlo?
Este comando abrirá un abanico de posibilidades para los proyectos. Desde personificación de movimientos y dinámicas, minijuegos, dinamismo, ahorro de tiempo con scripts y hasta el famoso follow me.
Para los curiosos que quieran saber como puede ser logrado esto, aquí les dejo la explicación. Por las dudas, no es necesario saber ni leer nada de lo que voy a explicar a continuación para poder utilizarlo.
Algoritmos de búsqueda:
Los algoritmos de búsqueda son un campo de la inteligencia artificial tradicional y son indispensables para resolver problemas en áreas tan diversas como la robótica, las telecomunicaciones, la clasificación de datos, los problemas lógico-matemáticos y por supuesto, los videojuegos.
Esto es básicamente un grafo de búsqueda:
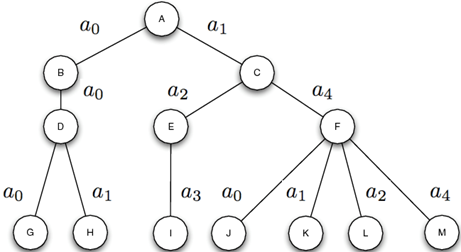
A partir de un nodo inicial vamos explorando los nodos hijo (o children) hasta que encontremos la solución que queremos.
Adaptar este grafo a nuestro problema es tan sencillo como definir los hijos de cada nodo como los posibles pasos que podría dar el mini (adelante, atrás, arriba, abajo) y nos encargaríamos de evaluar cuales de estos nodos hijos no son posibles de alcanzar (obstáculo, fuera del mapa, mini obstruyéndolo o diferencia de altura). Con la información del mapa y el estado de los overworld es más que suficiente para esta evaluación. Por lo que podemos concentrarnos en que además el camino que encuentre sea el óptimo siempre, es decir, el que lo lleve al destino con el menor número de pasos posibles.
¿Dijkstra, Best-First, A*?
Existen muchos tipos de algoritmos de búsqueda aplicada a árboles y grafos de búsqueda, los más simples son simplemente explorar cada una de las ramificaciones hasta llegar al fondo y seguir con la siguiente, de forma que por fuerza bruta nos topemos con la solución (Deep First Search). Sin embargo, además que gastamos un inmenso tiempo de computación no garantizamos que cuando demos con el goal el camino será el óptimo.
También existe la opción de explorar todos hijos primero e ir bajando en profundidad de todas las ramas al mismo tiempo. Este algoritmo se llama Breadth First Search (BFS), además, si usamos este método y a cada transición le damos un costo (como número de pasos) y a medida que vamos bajando en el árbol hacemos que el costo de los nodos sea más alto, podríamos entonces quedarnos con el goal que tenga el costo menor… Es más, podríamos diseñar una frontera donde almacenemos todos los nodos hijos que vamos descubriendo y los vamos eligiendo del menor al mayor costo total. De esta manera, la frontera va separando las casillas exploradas de las que aún no hemos explorado.
A este algoritmo se le conoce como algoritmo de Dijkstra o de los caminos mínimos, y es una genialidad, porque siempre nos asegura que la meta que encontremos será óptima, es decir que el camino que seguirá el mini al final será el del menor número de pasos…

Aun así, que el algoritmo sea óptimo, no significa que sea el mejor. Puesto que tenemos que barrer con casi todos los nodos y realizar muchas operaciones para encontrar el nodo final y el camino óptimo.


En las imágenes, podemos ver los nodos explorados en azul y la frontera en verde. Se puede notar que casi todo el mapa se ha explorado y que un ligero cambio de un tile puede hacer que todo el mapa sea explorado. Aún así, el algoritmo siempre escoge la ruta más corta entre el inicio y el destino. Izquierda: Número de pasos: 18, Número de operaciones: 120. Derecha: Número de pasos: 26, Número de operaciones: 130.
¿Qué importa si es óptimo? ¡Yo solo quiero que encuentre un camino y rápido!
Los mapas de los juegos de Pokemon guardan un detalle muy bueno ¡Los conocemos de antemano!, a menos que juegues Mundo Misterioso, sabes con antelación como será un mapa porque está compilado desde antes, eso nos puede traer una pequeña ventaja. ¿Y si en vez de calcular el número de pasos dados para cada nodo más bien calculamos la distancia que le falta para llegar a la meta?
A este tipo de búsqueda se le llama búsqueda informada, y si hacemos eso, estaríamos usando una heurística para calcular el costo, esta vez nos interesa reducir esa distancia (que la calculamos como en ejemplo de Petalia: distancia en horizontal más distancia en vertical) sin importar los obstáculos que haya (de eso ya se encarga el grafo al escoger los hijos posibles). Este es un algoritmo Best First. Como podrás darte cuenta, el uso de la heurística nos ha brindado información de la meta y como llegar a ella rápidamente, sin embargo, al no contar los pasos para el costo no estamos seguros si la solución a la que llegamos es óptima o no, solamente que hemos llegado rápido y sin hacer tantos cálculos.


Como vemos en las imágenes, los nodos explorados son muchísimo menos, es decir, se encuentra un resultado mucho más rápido y sin tanto coste computacional. Sin embargo, como vemos en la imagen de la derecha, el camino que ha encontrado no es el óptimo. Izquierda: Número de pasos: 18, Número de operaciones: 65. Derecha: Número de pasos: 28, Número de operaciones: 101.

¡ESPERA, soy perfeccionista! ¿No puedes darme un algoritmo que sea óptimo y que no haga tantos cálculos innecesarios?
Para los que lo quieren todo tenemos el maravilloso A* (se pronuncia a-star), que toma lo bueno del Dijkstra al llevar la cuenta de los costos de los nodos, pero también teniendo en cuenta la heurística del Best First.
Para hacer esto, a la hora de decidir a que nodo darle prioridad realiza la siguiente operación:
f(n) = g(n) + h(n)
Donde n es el nodo, f(n) es el valor sobre el que se discriminará el nodo n con respecto a los otros nodos. g(n) es el costo en pasos acumulado del nodo y h(n) es la heurística de dicho nodo con respecto al destino. Si da la casualidad de que dicha heurística es una subestimación del costo final (es decir que siempre será menor o igual al costo final) garantizaremos que el algoritmo será siempre óptimo.
De esta manera podemos jugar con el algoritmo para hacerlo más rápido para encontrar una solución o hacerlo más dado encontrar la solución óptima.
En mi código de la implementación dejo un peso que le pueden agregar a la heurística:
https://github.com/J2M2/pokeemerald/blob/8747f910aa52085469ded4dfcf0fe7e0c014e0d3/include/movement_path_planning.h#L30
#define HEUR_WEIGHT 1
Si es 0 tendrán Dijkstra, si es 1 será A* y si eligen un valor muy alto tendrán un Best First.
¿Qué resultado obtenemos con A*?


Izquierda: Número de pasos: 18, Número de operaciones: 78. Derecha: Número de pasos: 26, Número de operaciones: 113.
Si bien el número de operaciones es ligeramente mayor que el obtenido con el Best First, usando A* garantizamos que el camino siempre será óptimo y la heurística nos intentará reducir el número de operaciones hasta donde sea posible.


Podemos ver ambos ejemplos in-game en los gifs usando el algoritmo A* para encontrar el camino más corto.
Recuerden que esta explicación es únicamente para los más curiosos, no es para nada necesaria saber de esto para poder utilizarlo en sus hack roms.
Me alegra mucho volver a WAH a aportar mi granito de arena a este mundo que jamás ha podido salir de mi corazón. No se extrañen de verme más seguido en el foro, de que empiece a subir más aportes y tutoriales…. ¡Y de una sorpresa apocalíptica de un proyecto que tengo ya en desarrollo en decomp!
Si quieren estar al tanto sobre este nuevo comando, pueden acceder al tema de investigación del foro.
Saludos,
Juanjo
Comentarios